Τυπολόγιο

- Χρήστος Τσακμάκης
Κεφάλαιο 1: Κόστος Ευκαιρίας (Εναλλακτικό Κόστος)
- Χρήστος Τσακμάκης
Χαρακτηρισμός συνδυασμών
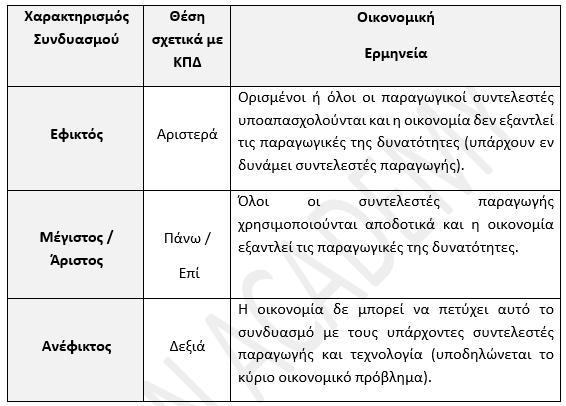
Να θυμάσαι:
- Ένας εφικτός συνδυασμός γίνεται μέγιστος όταν όλοι οι παραγωγικοί συντελεστές χρησιμοποιηθούν πλήρως και αποτελεσματικά.
- Ένας ανέφικτος συνδυασμός μπορεί μελλοντικά να επιτευχθεί αν:
- αυξηθούν οι ποσότητες των παραγωγικών συντελεστών,
- βελτιωθεί η τεχνολογία παραγωγής, ή
- συμβούν και τα δύο μαζί.
Μετατοπίσεις ΚΠΔ
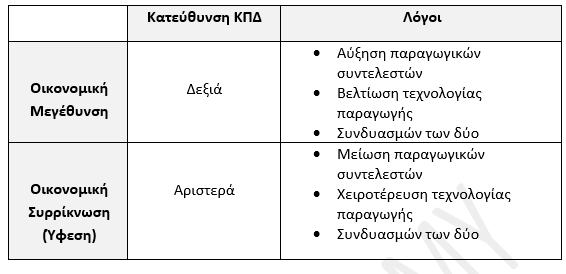
Να θυμάσαι:
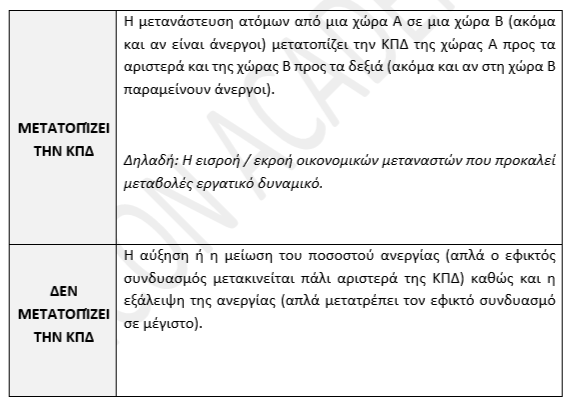
Κόστος Ευκαιρίας (Εναλλακτικό Κόστος)

Παρατηρήσεις:
- Ορισμός: Είναι όλα τα άλλα αγαθά που θυσιάστηκαν για την παραγωγή ενός προϊόντος και τα οποία θα μπορούσαν να είχαν παραχθεί με τους ίδιους συντελεστές παραγωγής.
- Ερμηνεία: Μας δείχνει πόσες μονάδες ενός αγαθού πρέπει να θυσιαστούν για να παραχθεί ΜΙΑ μονάδα από ένα άλλο αγαθό.
- Παράδειγμα: ΚΕΧ(σε όρους Ψ) = 4. Αυτό σημαίνει πως για να παραχθεί μια μονάδα του αγαθού Χ, θυσιάζονται 4 μονάδες του αγαθού Ψ.
- Χρηματικό Κόστος: Χρ.ΚΧ = ΚΕΧ * Τιμή πώλησης Ψ και Χρ.ΚΨ = ΚΕΨ * Τιμή πώλησης Χ
- Το ΚΕ εξ ορισμού είναι αρνητικός αριθμός και οφείλεται στην αρνητική σχέση των δύο αγαθών αφού όταν αυξάνεται η παραγωγή του ενός μειώνεται η παραγωγή του άλλου.
- Για καθαρά υπολογιστικούς λόγους, τα ΔΧ και ΔΨ τα υπολογίζουμε παίρνοντας πάντα τη θετική διαφορά, δηλαδή μεγαλύτερη τιμή – μικρότερη τιμή του πίνακα τόσο για το Χ, όσο και για το Ψ.
Χαρακτηρισμός ΚΕ
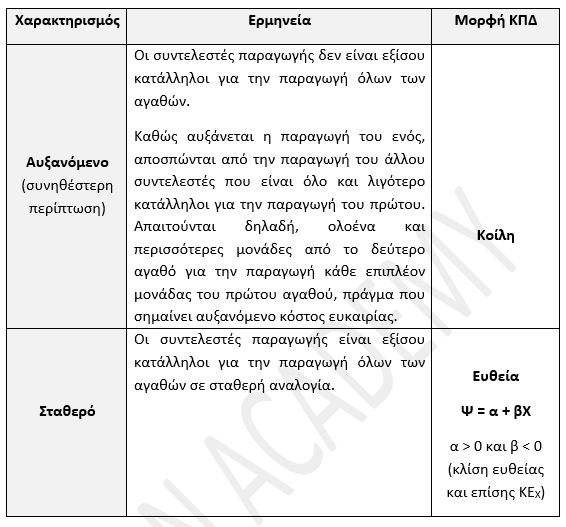
Να θυμάσαι:
- Το ΚΕ υπολογίζει ποσότητες που θυσιάζονται (όχι σε ποσοστό, όχι σε χρήματα) για την παραγωγή μιας μονάδας ενός αγαθού.
- Το ΚΕ υπολογίζεται μόνο μεταξύ μέγιστων / άριστων συνδυασμών.
- Όταν το υπολογίσουμε ανάμεσα σε δύο συνδυασμούς(πχ. Α και Β), τότε για όλους τους ενδιάμεσους συνδυασμούς από αυτούς παραμένει σταθερό.
- Όταν επιλέγουμε συνδυασμούς πχ για το ΚΕΧ, τους γράφουμε με τη φορά που το αντίστοιχο αγαθό (Χ) αυξάνεται. Πχ. ΚΕχ (ΒàΑ) και όχι (ΑàΒ).
- Το ΚΕ το εξετάζουμε (αν αυξάνεται ή μειώνεται) με την ίδια φορά που αυξάνεται η παραγωγή του αντίστοιχου αγαθού του.
- Ότι είναι το ΚΕ για το ένα αγαθό (πχ. αυξανόμενο), θα είναι το ίδιο και το ΚΕ για το άλλο αγαθό.
- Τα ΔΧ και ΔΨ τα υπολογίζουμε παίρνοντας πάντα τη θετική διαφορά, δηλαδή μεγαλύτερη ποσότητα – μικρότερη ποσότητα του πίνακα.

