Τυπολόγιο

 

I. ΥΠΟΛΟΓΙΣΜΟΣ ΕΥΘΕΙΑΣ ΚΑΙ ΓΡΑΦΙΚΗ ΑΠΕΙΚΟΝΙΣΗ

 Στα κεφάλαια 1, 2, 4, και 5 χρειάζεται σε αρκετές ασκήσεις να υπολογίσουμε την συνάρτηση όταν είναι ευθεία (γραμμική). Ο γενικός αλγεβρικός της τύπος είναι:

Υ = α + βΧ

Συγκεκριμένα έχουμε:

• Κεφάλαιο 1: Ψ = α + βΧ
• Κεφάλαιο 2: Q_D = α + βΡ (Συνάρτηση Ζήτησης)
• Κεφάλαιο 4: Q_S = γ + δΡ (Συνάρτηση Προφοράς)

Α τρόπος (ΣΥΣΤΗΜΑ)

Δημιουργούμε σύστημα 2 εξισώσεων με 2 αγνώστους από τις τιμές των αντίστοιχων μεταβλητών που συνήθως θα δίνονται σε κάποιο πίνακα σε εκφώνηση άσκησης ή κάποιον που φτιάξαμε εμείς με τα δεδομένα της.

Β τρόπος (ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ)

Αν έχουμε ένα σημείο και την κλίση λ (πχ. ΚΕ_Χ στο 1^ο κεφάλαιο) της ευθείας τότε χρησιμοποιούμε το γενικό τύπο της εξίσωσης της ευθείας

Υ – Υ₀ = λ (Χ – Χ₀)

 

όπου Χ₀, Ψ₀ το σημείο που θα έχουμε από την άσκηση.

Αν έχουμε δύο σημεία Α (Χ₁, Ψ₁) και Β (Χ₂, Ψ₂), τότε χρησιμοποιούμε τον παρακάτω τύπο: (Ψ-Ψ1) / (Χ-Χ1) = (Ψ2-Ψ1) / (Χ2-Χ1)

Για να σχεδιάσουμε την ευθεία (σε περίπτωση που μας το ζητάει η άσκηση) θα πρέπει να προσδιορίσουμε τα σημεία που τέμνει τους άξονες (οριζόντιο και κάθετο). Αυτό το πετυχαίνουμε μηδενίζοντας μια τη μια μεταβλητή και μια την άλλη.

Πχ. Για Χ = 0, Ψ =…  και για Ψ = 0, Χ=…

 

II. ΠΟΣΟΣΤΙΑΙΑ ΜΕΤΑΒΟΛΗ (%Δ)

 

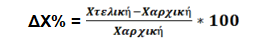
Αυτό το ερώτημα μπορεί να ζητηθεί ως: υπολογίστε την ποσοστιαία μεταβολή της συνολικής δαπάνης ΔΣΔ% (2^ο κεφ), του εισοδήματος ΔΥ% (2^ο κεφ), των εσόδων των παραγωγών ΣΕ_Π% (5^ο κεφ), κλπ. Απλά αλλάζουμε κάθε φορά την μεταβλητή για την οποία πρέπει να υπολογίσουμε την ποσοστιαία μεταβολή.

Σε περίπτωση που η άσκηση δίνει μια αρχική τιμή Χ και ζητάει μια αντίστοιχη μεταβολή της κατά κάποιο ποσοστό έχουμε:

 

(+ όταν αυξάνεται, και – όταν μειώνεται)

 

III. ΜΕΤΑΒΟΛΗ

 ΔΧ = Χ_τελική – Χ_αρχική

Οι παραπάνω τύποι μπορούν να έχουν εφαρμογή σε ασκήσεις όλων των κεφαλαίων όπως για παράδειγμα στην τιμή, το εισόδημα, τις ελαστικότητες, τα συνολικά έσοδα των παραγωγών, κλπ. Κάθε φορά αντικαθιστούμε στον αντίστοιχο τύπο τις τιμές των μεταβλητών που μας ζητάει η άσκηση.

 

III. ΜΕΤΑΒΟΛΗ

 ΔΧ = Χ_τελική – Χ_αρχική

Οι παραπάνω τύποι μπορούν να έχουν εφαρμογή σε ασκήσεις όλων των κεφαλαίων όπως για παράδειγμα στην τιμή, το εισόδημα, τις ελαστικότητες, τα συνολικά έσοδα των παραγωγών, κλπ. Κάθε φορά αντικαθιστούμε στον αντίστοιχο τύπο τις τιμές των μεταβλητών που μας ζητάει η άσκηση.

 

 V. ΥΠΟΛΟΓΙΣΜΟΣ ΡΙΖΩΝ 2ΒΑΘΜΙΑΣ ΕΞΙΣΩΣΗΣ

 αx² + βx + γ = 0

 

Διακρίνουσα: Δ = β² - 4αγ

Οι ρίζες θα είναι: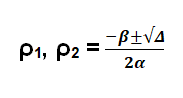 

 

(θα επιλέγουμε τη ΘΕΤΙΚΗ!)

 

Παρατήρηση:

 

Αυτή η περίπτωση θα χρειαστεί πχ. στο 5^ο κεφάλαιο, για να βρούμε σημείο ισορροπίας όταν η συνάρτηση ζήτησης θα έχει τη μορφή ισοσκελούς υπερβολής.